The Model
The idea of the diffuse interface
goes back to van der Waals who proposed square-gradient theory of the
interface. The dynamic generalizations of the models of that type
have been proposed in works of
B. U. Felderhof,
J. S. Langer and L. A. Turski,
D. M. Anderson, and, perhaps, others.
The set of dynamical equations comprises conservation of mass:
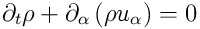 ,
,
conservation of momentum:
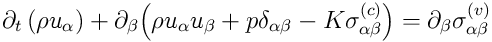 ,
,
and equation for the entropy density
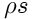 :
:
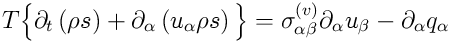 ,
,
where
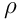 is the medium mass density,
is the medium mass density,
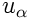 is the velocity,
is the velocity,
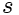 is the specific entropy (entropy per unit mass),
is the specific entropy (entropy per unit mass),
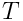 is the temperature,
is the temperature,
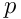 is the thermodynamic pressure, and
is the thermodynamic pressure, and
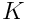 is the constant related to the liquid-vapor surface tension. Greek
indices label vector and tensor components in Cartesian
coordinates and the familiar summation convention
is the constant related to the liquid-vapor surface tension. Greek
indices label vector and tensor components in Cartesian
coordinates and the familiar summation convention
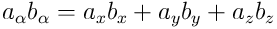 is understood;
is understood;
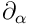 stands for
stands for
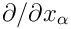 and
and
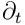 denotes partial derivative with respect to the time
denotes partial derivative with respect to the time
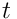 .
.
The viscous stress tensor
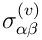 is supposed to be of the Newtonian form
with bulk viscosity set to zero
is supposed to be of the Newtonian form
with bulk viscosity set to zero
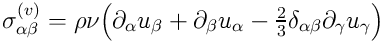 .
.
The heat flux
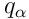 is given by the Fourier Law
is given by the Fourier Law
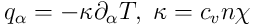 .
.
In the last formula
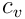 is the specific heat for constant volume,
is the specific heat for constant volume,
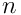 is the particle density (i.e.,
is the particle density (i.e.,
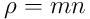 , where
, where
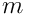 is the particle mass). Kinematic viscosity
is the particle mass). Kinematic viscosity
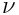 as well as thermal diffusivity
as well as thermal diffusivity
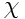 are assumed constant.
are assumed constant.
Momentum equation coincides with the
classical Navier-Stokes equation except of the capillary stress tensor
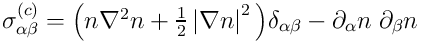 ,
,
which models the forces associated with the interface.
The above system of equations must be supplemented by two
equations of state:
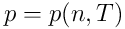 and
and
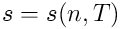 .
We use van der Waals approximate formulas with parameters
characteristic for argon in that place.
.
We use van der Waals approximate formulas with parameters
characteristic for argon in that place.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() is supposed to be of the Newtonian form
with bulk viscosity set to zero
is supposed to be of the Newtonian form
with bulk viscosity set to zero
![]() .
.![]() .
.![]() ,
,![]() and
and
![]() .
We use van der Waals approximate formulas with parameters
characteristic for argon in that place.
.
We use van der Waals approximate formulas with parameters
characteristic for argon in that place.