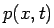Fleming-Viot Processes

We consider the system of the Brownian particles confined in a box whose boundaries act as a sink of the particles. The annihilation rate at the boundaries is matched by the branching (birth) rate in the bulk, thus the total number of the particles is preserved. The process can be described in terms of the probability distribution function 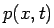, which evolves according to the following equation

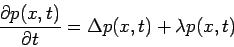
and vanishes at the container boundaries. The first term in the right hand side describes diffusion of the particles, and the second one represents the branching process. The constant 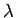can be viewed as the Lagrange multiplier controlling normalization of :

.

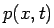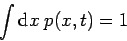It turns out that the dynamics of the process can be conveniently interpreted in terms of the Renyi entropy

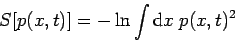
and the Renyi entropy production

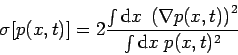
Namely, the Renyi entropy production is monotonically decreasing function of time irrespective of the initial conditions. In the steady state it is equal to the lowest eigenvalue of the Dirichlet Laplacian. More details can be found in our paper.

All the movies below have been encoded with MEncoder. To watch the movies, the DivX codec must be installed on your system.

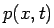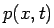Shown is the time evolution of the probability distribution function for two different container geometries. The green-orange colormap is used to visualize the value of . In the top pannel of each movie the Fleming-Viot process is presented, while in the bottom one, regular diffusion evolving from the same initial configuration is shown.

The last movie concerns one possible generalization of the process described above, in which many types (colors) of the Brownian particles are allowed. When particles of different colors collide, both annihilate instantiously. At the same time, randomly chosen particles of the corresponding colors are branched. This way the total number of the particles of each color is preserved.