Lattice Boltzmann simulations
|
|
V. Babin and R. Holyst
|
The
Lattice Boltzmann approach has attracted much attention
recently, hence, we have also followed this direction.
Using the algorithm proposed by
C. Denniston, D. Marenduzzo, E. Orlandini, J. M. Yeomans, we
have simulated the process of defects
annihilation in nematic liquid crystals.
In addition, we have also implemented the lattice Boltzmann simulator of the
familiar liquid/vapor flows
(see
Michael R. Swift, W. R. Osborn, J. M. Yeomans).
The source code can be downloaded here.
All the movies below have been encoded
with MEncoder.
To watch the movies, the
DivX codec must be installed
on your system.
|

movie (4.3 Mb)
|
Annihilation of four dislocation lines in a nematic liquid
crystal. Shown is the evolution of the aligment tensor. The values
of the tensor are represented by ellipsoids so that the axes of the
ellipsoid are directed along the eigenvectors of the aligment tensor,
while their lengths are proportional to the corresponding eigenvalues.
The movie frames are rendered using
POV-Ray.
Notice the anisotropy of defects speed, which is due to
the backflow.
|
|

movie (16 Mb)
|
Spinodal decomposition of the two-dimensional non-ideal fluid
(with the van der Waals equation of state) in the shear
flow. Shown is the time evolution of the density.
The red-white-blue colour-map is used to visualize the magnitude of
the fluid density. The size of the simulation box is 512x288. Periodic
boundary conditions in horizontal direction are assumed.
|
|
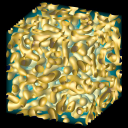
movie (4.5 Mb)
|
Spinodal decomposition of the non-ideal fluid
(with the van der Waals equation of state).
Shown is the time evolution of the density.
The light/dark blue colour-map is used to visualize the magnitude of
the fluid density. The level surface, corresponding to the
liquid/vapor interface, is also shown. The movie frames are rendered
using OpenDX. The size of the
simulation box is 160x160x160, and the periodic
boundary conditions in all three dimensions are assumed.
|


