3D Patterns in Nonextensive Thermodynamics
|
|
O. Cybulski, D. Matysiak, V. Babin, R. Holyst
|
We investigate a system of many Brownian particles confined in a
cubic periodic box. The particles are grouped into two types, a and b.
When two particles of different type meet, they instantaneously
annihilate each other and disappear from the system. At the same time,
when any particle of a given type is removed (due to annihilation),
another particle of the same type (chosen at random) is duplicated, i.e.
gives birth to a new particle of the same type. Thus, the number of
particles of each type is conserved. Diffusion, together
with annihilation of particles of different type, leads to the spatial
segregation of particles of different type.
In the continuous limit, we can describe the process in terms of the
evolution of the probability density distributions, pa and pb.
The densities pa and pb satisfy the following equations:
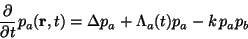
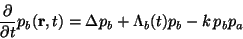 ,
where the positive constant k acts as the chemical reaction rate
constant. The terms
,
where the positive constant k acts as the chemical reaction rate
constant. The terms 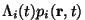 represent
"birth" of i-type particles at point r at time t. The
functions
represent
"birth" of i-type particles at point r at time t. The
functions 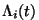 must be determined from the
normalization condition
must be determined from the
normalization condition
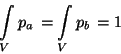 .
The constant k represents annihilation of particles of different type.
For finite values of k, the domains occupied by particles of
different type partially overlap. When k increases, the shape of
domains does not change, but the boundaries get sharper.
As k approaches infinity, we are left with a model with infinitely sharp
separation of the particles of different type. In this setup, papb=0.
The stationary states correspond to eigenfunctions of the Laplacian. While it has a very large number of solutions, the evolutions leads to only a few specific stationary states, and only one of these, where the interface between domains forms topological surface P, was found to be stable for non-trivial cases (sin(X) and sin(X)+sin(Y) were also found to be stable).
Below we present plots of the evolution of the Renyi entropy production, expressed as
.
The constant k represents annihilation of particles of different type.
For finite values of k, the domains occupied by particles of
different type partially overlap. When k increases, the shape of
domains does not change, but the boundaries get sharper.
As k approaches infinity, we are left with a model with infinitely sharp
separation of the particles of different type. In this setup, papb=0.
The stationary states correspond to eigenfunctions of the Laplacian. While it has a very large number of solutions, the evolutions leads to only a few specific stationary states, and only one of these, where the interface between domains forms topological surface P, was found to be stable for non-trivial cases (sin(X) and sin(X)+sin(Y) were also found to be stable).
Below we present plots of the evolution of the Renyi entropy production, expressed as
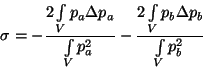 ,
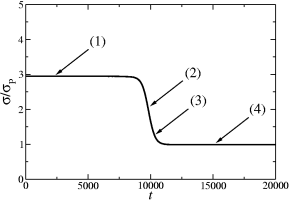
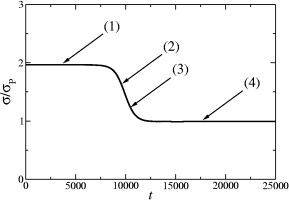
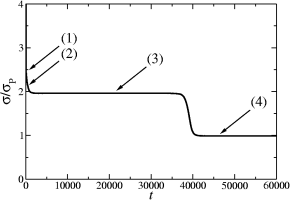
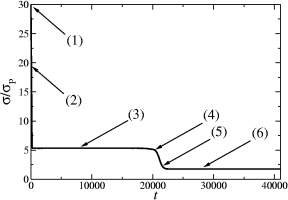
of systems which were initialized in such a way that the interface between the domains of different type form topological surfaces D, G, I-WP and F-RD. As can be seen, the entropy production decreases monotonically in time. Plateaus correspond to stationary states and eigenfunctions of the Laplacian. The value of the entropy production at the plateaus correspond to eigenvalues of the Laplacian. Also provided are movies showing the critical moments (particularly transitions from one plateau to another) during the evolution of the system.
Movies
The entopy production plots and movies correspond to initial interface surfaces D, G, I-WP and F-RD, respectively.
All the movies below have been encoded
with MEncoder.
To watch the movies, the
DivX codec must be installed
on your system.
For more details, please refer to our paper [JCP submitted].
,
of systems which were initialized in such a way that the interface between the domains of different type form topological surfaces D, G, I-WP and F-RD. As can be seen, the entropy production decreases monotonically in time. Plateaus correspond to stationary states and eigenfunctions of the Laplacian. The value of the entropy production at the plateaus correspond to eigenvalues of the Laplacian. Also provided are movies showing the critical moments (particularly transitions from one plateau to another) during the evolution of the system.
Movies
The entopy production plots and movies correspond to initial interface surfaces D, G, I-WP and F-RD, respectively.
All the movies below have been encoded
with MEncoder.
To watch the movies, the
DivX codec must be installed
on your system.
For more details, please refer to our paper [JCP submitted].
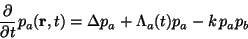
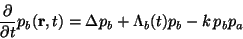 ,
,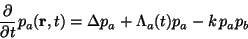
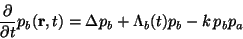 ,
,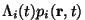 represent
"birth" of i-type particles at point r at time t. The
functions
represent
"birth" of i-type particles at point r at time t. The
functions 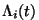 must be determined from the
normalization condition
must be determined from the
normalization condition
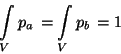 .
.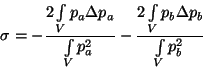 ,
,